What Is Bootstrapping In Statistics?

If you’ve ever dived into the fascinating world of statistics, you may have come across the term “bootstrapping.” But what exactly is bootstrapping in statistics? Well, my friend, let me break it down for you in a way that’s both informative and entertaining.

Imagine you’re at a party, and everyone is talking about this fabulous new statistical technique called bootstrapping. It’s like the life of the statistical party! Bootstrapping is a resampling method that allows us to estimate the variability of a statistic by repeatedly sampling from our original dataset. It’s like taking that dataset, putting it in a fancy statistical blender, and creating a whole bunch of new samples. Each of these samples is like a mini version of the original dataset, and by analyzing them, we can get a sense of how our statistic might vary if we were to collect multiple samples from the population.

Now, I know what you’re thinking. “Why go through all this trouble? Can’t we just stick to the original dataset?” Well, my curious friend, the beauty of bootstrapping lies in its ability to work with small datasets or situations where assumptions about the distribution of the data may not hold. It’s like having a statistical Swiss Army knife in your pocket – versatile, reliable, and ready to tackle any uncertainty. So, the next time you hear the term bootstrapping in statistics, you can confidently join the conversation and impress your friends with your newfound statistical knowledge.

What is Bootstrapping in Statistics?

Bootstrapping is a statistical technique that involves sampling data repeatedly from a given dataset to estimate the variability of a statistic. It is a resampling method that allows researchers to make inferences about a population without making any assumptions about the underlying distribution of the data. This technique is particularly useful when dealing with small sample sizes or when the data does not meet the assumptions of traditional statistical tests.

How Does Bootstrapping Work?

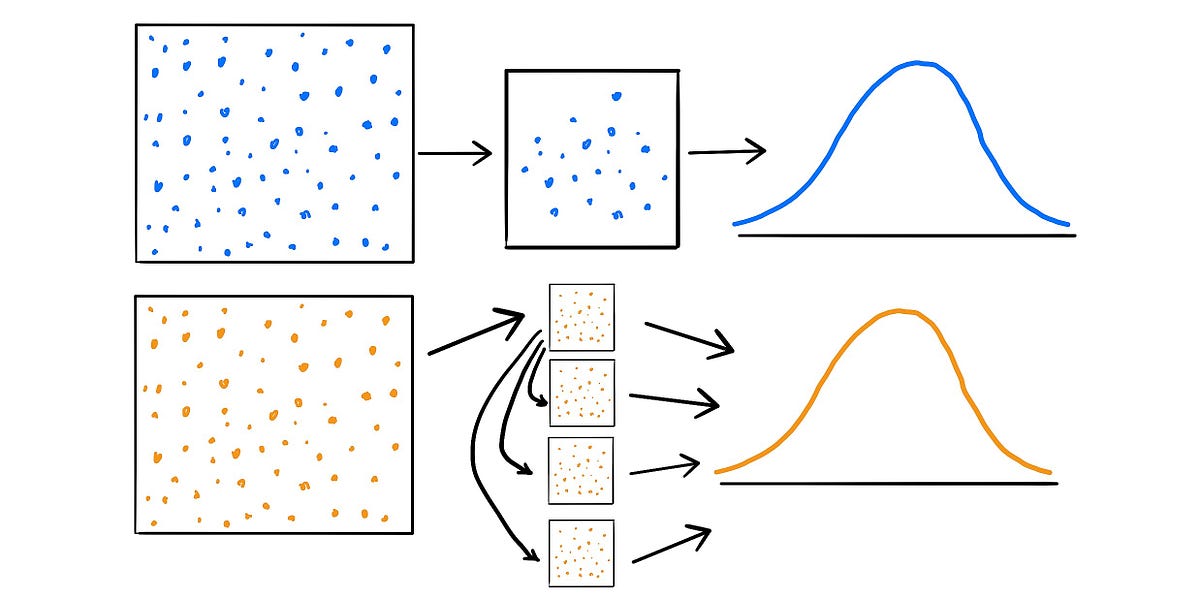
To understand how bootstrapping works, let’s consider a simple example. Suppose we want to estimate the average height of all adults in a certain population. We collect a sample of 100 individuals and calculate the mean height. However, we know that this sample is just one possible representation of the population, and there is inherent variability in the data.

Bootstrapping allows us to create multiple “bootstrap samples” by randomly selecting individuals from the original sample with replacement. This means that each bootstrap sample can contain the same individual multiple times or not at all. We then calculate the mean height for each bootstrap sample and obtain a distribution of means. From this distribution, we can estimate properties such as the standard error, confidence intervals, and hypothesis tests.

The Benefits of Bootstrapping

Bootstrapping offers several benefits compared to traditional statistical methods. First, it does not assume any specific distribution for the data, making it more robust and applicable to a wide range of situations. Second, it provides a more accurate estimation of variability by directly using the observed data. This is particularly useful when the assumptions of parametric tests, such as normality or homogeneity of variances, are not met. Lastly, bootstrapping allows for the estimation of confidence intervals, which provide a measure of uncertainty around the estimated statistic.

Steps to Perform Bootstrapping

To perform bootstrapping, follow these steps:

1. Randomly select a sample from the original dataset, with replacement, to create a bootstrap sample.
2. Calculate the desired statistic (e.g., mean, median, correlation) for the bootstrap sample.
3. Repeat steps 1 and 2 a large number of times (e.g., 1000) to obtain a distribution of the statistic.
4. Analyze the distribution to estimate the variability of the statistic, such as confidence intervals or hypothesis tests.

Bootstrapping can be implemented using statistical software like R, Python, or specialized bootstrapping packages. These tools automate the resampling process and provide easy-to-use functions for calculating bootstrap statistics.

Applications of Bootstrapping

Bootstrapping has a wide range of applications in various fields of study. Here are a few examples:

Economics

In economics, bootstrapping can be used to estimate the variability of economic indicators such as Gross Domestic Product (GDP), inflation rates, or stock market returns. By resampling historical data, economists can gain insights into the uncertainty surrounding these indicators and make more informed decisions.

Biostatistics

In biostatistics, bootstrapping is often used in survival analysis, where researchers analyze time-to-event data, such as patient survival times. Bootstrapping can provide more accurate estimates of survival probabilities and hazard ratios, even when the assumptions of traditional survival models are not met.

Machine Learning

Bootstrapping is also popular in the field of machine learning. It is used to estimate the performance of predictive models by resampling the data and calculating metrics such as accuracy, precision, and recall. Bootstrapping can help assess the stability and variability of a model’s performance and guide model selection.

Environmental Sciences

In environmental sciences, bootstrapping can be applied to estimate the uncertainty in ecological models or climate predictions. By resampling data from monitoring stations or climate simulations, scientists can quantify the variability in their models and provide more reliable estimates of future trends.

Conclusion

Bootstrapping is a powerful statistical technique that allows researchers to estimate the variability of a statistic without making strong assumptions about the data. By resampling from the original dataset, bootstrapping provides more accurate estimates of uncertainty and can be applied to a wide range of fields and research questions. Whether you are analyzing economic indicators, survival data, machine learning models, or environmental trends, bootstrapping can enhance your statistical analyses and provide valuable insights. So next time you encounter a small sample size or non-normal data, consider using bootstrapping to unlock the full potential of your analysis.

Frequently Asked Questions

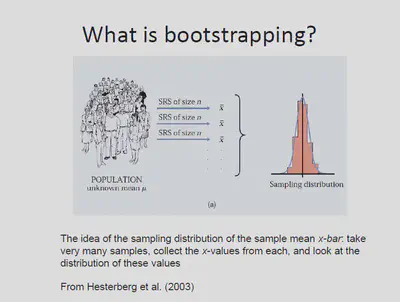
Bootstrapping in statistics is a resampling method used to estimate the uncertainty of a statistic or to make inferences about a population based on a sample. It involves repeatedly sampling with replacement from the original sample to create new samples, calculating the statistic of interest for each new sample, and then analyzing the distribution of these statistics.

Question 1: How does bootstrapping work?

Bootstrapping works by simulating the process of sampling from a population using the available sample. It involves randomly selecting observations from the original sample with replacement, which means that an observation can be selected multiple times or not selected at all in each new sample. This process is repeated many times to create a distribution of statistics that can be used to estimate the uncertainty of the statistic of interest.

By generating multiple bootstrap samples and calculating the statistic of interest for each sample, we can obtain an empirical distribution for the statistic. This distribution can then be used to estimate confidence intervals, test hypotheses, or assess the variability of the statistic.

Question 2: What are the advantages of bootstrapping?

One of the main advantages of bootstrapping is that it does not rely on assumptions about the underlying population distribution. It is a non-parametric method, meaning that it makes minimal assumptions about the shape, variability, or other characteristics of the population. This makes bootstrapping applicable in a wide range of situations.

Bootstrapping also provides a robust way to estimate the uncertainty of a statistic. It takes into account the variability within the sample and allows for the possibility of sampling error. By generating multiple bootstrap samples, bootstrapping captures the inherent uncertainty in sampling and provides a more accurate estimate of the variability of the statistic.

Question 3: When is bootstrapping useful?

Bootstrapping is useful in various statistical analyses and applications. It can be used to estimate confidence intervals for a statistic, which provide a range of plausible values for the population parameter. These confidence intervals can be particularly useful when the underlying population distribution is unknown or non-normal.

Bootstrapping is also valuable in hypothesis testing. It allows for the calculation of p-values by comparing the observed statistic to the distribution of bootstrapped statistics. This enables researchers to assess the significance of their findings without relying on specific assumptions about the population distribution.

Question 4: Are there any limitations to bootstrapping?

While bootstrapping is a powerful resampling method, it does have some limitations. One limitation is that it assumes the original sample is representative of the population. If the sample is biased or does not accurately reflect the population, bootstrapping may lead to biased estimates.

Another limitation is the computational intensity of bootstrapping. Since it involves generating multiple bootstrap samples, calculating the statistic of interest for each sample, and analyzing the distribution of these statistics, bootstrapping can be computationally demanding, especially for large datasets or complex statistical models.

Question 5: Can bootstrapping be used for any type of data?

Bootstrapping can be applied to various types of data, including numerical, categorical, and even time series data. It is a versatile method that does not require specific assumptions about the data distribution or structure. However, the effectiveness of bootstrapping may depend on the nature of the data and the research question.

For example, bootstrapping may be less effective for small sample sizes, as the resampling process may not adequately capture the variability in the population. Additionally, certain types of data, such as highly correlated or dependent data, may require specialized bootstrapping techniques to account for the specific structure of the data.

Final Summary: Understanding the Magic of Bootstrapping in Statistics

In the world of statistics, bootstrapping is like a magician’s trick that allows us to perform incredible feats with data. It’s a powerful technique that enables us to make accurate inferences about a population, even when our sample size is small. By resampling from our existing data, bootstrapping provides us with a glimpse into the possibilities and uncertainties that lie within our dataset.

Bootstrapping is like having a bag of tricks at our disposal. It allows us to estimate parameters, construct confidence intervals, and even assess the performance of our statistical models. With each resample, we create a mini-universe that reflects the complexities and variations of our original data. This enables us to understand the variability inherent in our sample and make robust conclusions about the population we’re studying.

So, the next time you find yourself grappling with a small sample size or uncertain about the generalizability of your findings, remember the magic of bootstrapping. It’s a statistical tool that empowers us to unlock valuable insights and make informed decisions. Just like a magician’s trick, bootstrapping reveals the hidden wonders within our data, elevating our understanding of the world around us. Embrace the power of bootstrapping, and let it guide you on your statistical journey.